Testing of Hypothesis- Lecture 1 (4th semester)

" Truth can be stated in a thousand different ways, yet each one can be true ..." - Swami Vivekananda

Consider the following hypothetical situation:

From previous experience we know that the birth weights of babies in England are Normally distributed with a mean of 3000 g and a standard deviation of 500 g.

We think that maybe babies in Australia have a mean birth weight greater than 3000 g and we would like to test this hypothesis.

The main hypothesis that we are most interested in is the research hypothesis, denoted H1, that the mean birth weight of Australian babies is greater than 3000 g.

The other hypothesis is the null hypothesis, denoted H0, that the mean birth weight is equal to 3000 g.

In summary:

H0 : µ = 3000g

H1 : µ > 3000g

The research hypothesis is often called the alternative hypothesis.

Here µ is considered as the population mean or average birth weight of Australian babies.

We start with the research hypothesis and ”set up” the null hypothesis to be directly counter to what we hope to show.

We then try to show that the null hypothesis is false, in light of our collected sample or sample data, In order to do that we first collect sample data from the population of our interest. Then we extract useful information from the data finally decide whether to reject or not to reject the null hypothesis.

Imagine that you take a sample of 44 babies from Australia, measure their birth weights and observe that the sample mean of these 44 weights is 3275 g. Suppose one of your friend who is also interested in this study take another sample of size 1121 and finds the sample mean is 3040 g. In this particular problem we are interested in population mean of birth weight of all Australian babies, thus it is our common intuition that we will make our decision on the basis of our observed sample mean. Now sample mean varies as sample observations are collected randomly from the population. So, we need a well defined decision rule to make our decision on the basis of our sample or data collected. For example, we set up a rule that if we find the sample mean is higher than 3050 g then we will consider that average birth weight of the Australian babies are higher than 3000 g, that is we reject the null hypothesis.

Working with this kind of predefined decision rule, we have to face two kind of problems. In the following sections we will discuss them with little elaboration. For now, to get the sense of that, just go through the previous paragraph. You and your fried both have collected the data. According to the predefined decision rule you will reject the null hypothesis, as your sample mean is 3275 g > 3050 g. On another hand your friend will not reject null hypothesis, as he got sample mean 3040 g < 3050 g. Now, your friend can claim that his sample size is much higher (as he has collected more data than you) and his decision is right not yours, because you got a few over weight babies in your small sample by chance. Now, your friends' claim might be true, because he has collected 20 times more data than you. From this incident, one thing is very clear that we have to be careful about the fact that our sample may mislead us, by chance. Because most of the time we don't know how much data is needed to get the idea about a certain property of the population of interest.

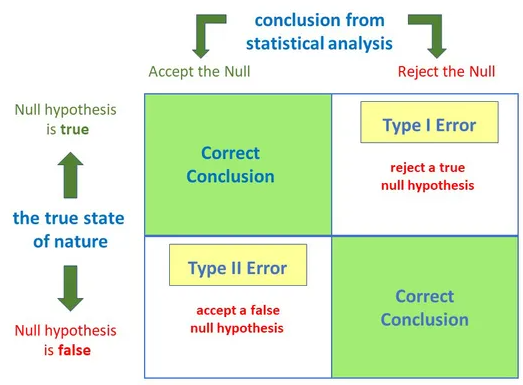
There are two types of errors we can commit in hypothesis testing. If we reject H0 when it is true, this is an error. It is called a Type 1 error.

If H0 is not true, i.e. H1 is true and we fail to reject H0, then this is also an error. It is termed as Type II error.